O(n) Random Sampling Graph Layouts

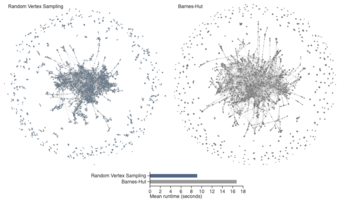
Using random sampling I developed d3-force-sampled, a D3.js module, to compute force-directed graph layouts about three times faster than the standard algorithm. The standard algorithm runs in O(n log(n)) time and space, whereas my algorithm is O(n) time and space. The difference is that the standard algorithm uses the Barnes-Hut approximation to calculate very accurate forces, but this generates a spacial tree in O(n log(n)) time that occupies O(n log(n)) space every iteration. In contrast, my algorithm approximates forces by sampling n^(3/4) vertices to update at an iteration and then sampling n^(1/4) vertices to use for calculating Coulombic forces. The algorithm works surprisingly well, although the layouts can look more random and less symmetric. Running ten iterations of the Barnes-Hut algorithm afterwards is enough to resolve the low-level randomness, and it is nearly as fast as the pure random sampling algorithm.

I attempted to use a similar approach to speed up spring force calculation, but the results were not satisfying. I reduced the overall runtime for all iterations from O(i * e) to O(e). But this only translated to at most a 10% runtime improvement in practice, and it came at the cost of substantially reducing the layout quality.

Live examples

• EuroVis 2019 Twitter interaction network
• Composing multiple forces and constraints with Random Vertex Sampling
• Random Vertex Sampling vs. Barnes-Hut Approximation
• Linear-time force-directed graph layouts with random vertex sampling

Blogs

Graph Layout by Random Vertex Sampling

Code

• d3-force-sampled GitHub repo
• Vertex sampling experiment and analysis
• Edge sampling experiment and analysis

Papers

Robert Gove. “A Random Sampling O(n) Force-calculation Algorithm for Graph Layouts.” Computer Graphics Forum 2019 (proc. EuroVis). [pdf] [osf]

Robert Gove. “Force-Directed Graph Layouts by Edge Sampling.” Large Data Analytics and Visualization 2019. [pdf] [osf]